SOAL FUNGSI: LINEAR, KUADRAT, RASIONAL, IRASIONAL DAN GRAFIKNYA SERTA MEMBACA GRAFIKNYA

 

NAMA : CHAMELIA CHANSA

KELAS  : X IPS 3

ABSEN : 08

Soal 1

 Diketahui fungsi linear f : x -> f(x) = ax + bdengan nilai f(0) = 2 dan nilai f(3) = 8.

a. Hitunglah nilai a dan b. Kemudian tuliskan rumus untuk fungsi f(x)
b. Tentukan titik-titik potong fungsi f dengan sumbu x maupun sumbu y
c. Gambarkanlah grafik fungsi f pada bidang Cartesius untuk daerah asal 
                                                                                                               
Pembahasan
Jawaban a
f(x) = ax + b
saat f(0) = 2, akan diperoleh:
0 + b = 2
b = 2
saat f(3) = 8, akan diperoleh:
3(a) + b = 8
3a + b = 8
3a + 2 = 8
3a = 6
a  = 2
Karena nilai a = 2 dan b = 2, maka rumus untuk fungsi f(x) adalah sebagai berikut
f(x) = ax + b
f(x) = 2x + 2

Jawaban b
y = f(x) = 2x + 2
Titik potong dengan sumbu x diperoleh apabila nilai y = 0
y = 2x + 2
0 = 2x + 2
2x = -2
x = -1
Sehingga koordinat titik dimana y = 0 adalah [-1, 0]
Titik potong dengan sumbu y diperoleh apabila nilai x = 0
y = 2x + 2
y = 2(0) + 2
y = 0 + 2
y = 2
Sehingga koordinat titik dimana x = 0 adalah [0, 2]
Dengan demikian, kurva grafik fungsi y = f(x) = 2x + 2 akan memotong sumbu x di titik [-1, 0] dan memotong sumbu Y di titik [0, 2].

Jawaban c
Karena titik potong pada sumbu-x dan sumbu-y sudah diketahui, maka kita dapat melukiskan grafik fungsi y = f(x) = 2x + 2 untuk x ∈ R pada bidang Cartesius. Gambar grafik fungsi tersebut adalah sebagai berikut.

Soal 2 

Koordinat titik balik grafik fungsi kuadrat $f\left(x\right)=2x^2-4x+5$ adalah $\cdots \cdot$
A. $(1,3)$                       D. $(2,5)$
B. $(1,5)$                       E. $(2,7)$
C. $(1,7)$

Pembahasan

Karena $f\left(x\right)=2x^2-4x+5$, berarti $a=2,b=-4,c=5$.
Absis titik balik dinyatakan oleh
$x_p=-\frac{b}{2a}=-\frac{-4}{2\left(2\right)}=1$
Substitusikan $x=1$ pada $f\left(x\right)=2x^2-4x+5$, sehingga diperoleh
$y_p=f\left(1\right)=2(1{)}^2-4(1)+5=3$
Jadi, koordinat titik balik grafik fungsi kuadratnya adalah 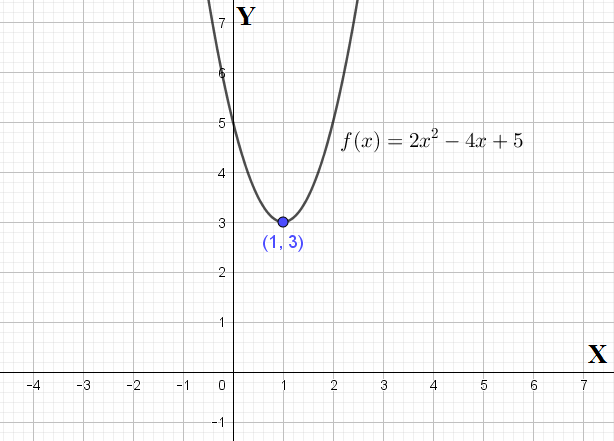$(x_p,y_p)=(1,3)$

(Jawaban A)

Soal 3

Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Untuk y = 1/x dalam kuadran III,

1. Mendeskripsikan sifat dari ujung grafik fungsi tersebut.
2. Mendeskripsikan apa yang akan terjadi pada saat x mendekati nol.

Pembahasan Serupa dengan sifat grafiknya pada kuadran I, maka akan kita peroleh

1. Pada saat x mendekati negatif tak hingga, nilai y akan mendekati nol. Jika disimbolkan akan menjadi: x → –∞, y → 0.
2. Pada saat x mendekati nol dari kiri, nilai y akan mendekati negatif tak hingga. Pernyataan tersebut juga bisa kita tuliskan dengan simbol x → 0–, y → –∞.

Fungsi y = 1/x²

Dari pembahasan di atas, kita bisa mengetahui bahwa grafik dari fungsi ini akan mengalami jeda pada saat x = 0.

Namun demikian, sebab kuadrat dari sembarang bilangan negatif merupakan bilangan positif, cabang-cabang dari grafik fungsi ini akan terletak kdi atas sumbu-x.

Perhatikan bahwa fungsi y = 1/x² adalah fungsi genap.

Sama halnya dengan y = 1/x, nilai x yang mendekati positif tak hingga akan menghasilkan y yang mendekati nol. Jika kita tulis simbolnya maka akan menjadi: x → ∞, y → 0.

Hal ini adalah salah satu indikasi dari sifat asimtot dalam arah horizontal. Serta kita akan menyatakan y = 0 adalah asimtot horizontal dari fungsi y = 1/x dan y = 1/x². Secara umum,

Asimtot Horizontal
Diberikan sebuah konstanta k, garis y = k adalah asimtot horizontal dari fungsi V(x) apabila x bertambah tanpa batas, akan menimbulkan V(x) mendekati k: x → –∞, V(x) → k atau x → ∞, V(x) → k.

Pada gambar (a) di bawah ini menggambarkan garis asimtot horizontal pada y = 1, yang menunjukan grafik f(x) sebagai translasi grafik y = 1/x ke atas sejauh 1 satuan.

Gambar (b) menggambarkan garis asimtot horizontal pada y = –2, yang menunjukan grafik g(x) sebagai pergeseran grafik y = 1/x² ke bawah sejauh 2 satuan.

Soal 4 

Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Berdasarkan gambar (b) di atas, pakailah notasi matematika guna:

1. Mendeskripsikan sifat dari ujung grafik di atas.
2. Mendeskripsikan apa yang berlangsung pada saat x mendekati nol.

Pembahasan

1. Pada saat x → –∞, g(x) → –2. Ketika x → ∞, y → –2.
2. Pada saat x → 0–, g(x) → ∞. Ketika x → 0+, y → ∞.

Dari contoh 2b di atas, maka dapat diketahi bahwasannya pada saat x mendekati nol, g akan berubah menjadi sangat besar serta semakin bertambah tidak terbatas.

Hal tersebut adalah indikasi dari sifat asimtot dalam arah vertikal.

Dan kemudian kita akan menyebut garis x = 0 adalah asimtot vertikal untuk g (x = 0 juga adalah asimtot vertikal untuk f). Secara umum,

Asimtot Vertikal
Diberikan sebuah konstanta h, garis x = h adalah asimtot vertikal untuk fungsi V apabila x mendekati h, V(x) akan bertambah atau berkurang tanpa batas: pada saat x → h+, V(x) → ±∞ atau pada saat x → h–, V(x) → ±∞.

Mengidentifikasi dari asimtot horizontal dan vertikal sangatlah bermanfaat.

Sebab grafik y = 1/x dan y = 1/x² bisa ditransformasi dengan menggesernya ke arah vertikal maupun gorizontal. Fungsi,

adalah bentuk pergeseran dari fungsi y = 1/x. Sementara untuk fungsi,

adalah bentuk pergeseran dari fungsi y = 1/x². Kemudian perhatikan contoh yang ada di bawah ini:

Soal 5

Perhatikan gambar di bawah!

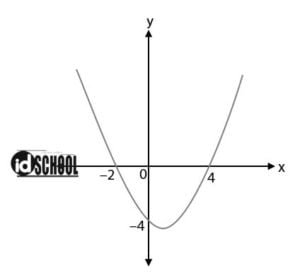
Persamaan grafik fungsi kuadrat pada gambar di atas adalah ….
A.   y = x² – ½x – 8
B.   y = x² – ½x – 4
C.   y = ½x² – x – 4
D.   y = ½x² – x – 8
E.   y = ½x² – 2x – 8

Pembahasan:

Diketahui dua titik yang memotong sumbu x adalah  (–2, 0) dan (4, 0). Diketahui juga sebuah titik pada grafik fungsi kuadrat (0, –4).

Mencari nilai A:
y = a (x – x1)(x – x2)
–4 = a(0 – (–2))(0 – 4)
–4 = a × 2 × (–4)
–4 = a(–8)
a = –4/–8
a = ½

Mencari persamaan kuadrat:
y = a(x – x1)(x – x2)
y = ½ (x + 2)(x – 4)
y = ½ (x² – 2x – 8)
y = ½x² – x – 4

Jadi, persamaan grafik fungsi kuadrat pada gambar di atas adalah y = ½x² – x – 4.

Jawaban: C