LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

 NAMA : CHAMELIA CHANSA

ABSEN : 08

KELAS : X IPS 3

LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

Untuk mencari luas suatu bangun datar (poligon), yang kita lakukan biasanya adalah mencari luas segitiga-segitiga kecil yang menyusun poligon tersebut. Tentunya kita tahu bagaimana rumus suatu segitiga. Banyak sekali rumus-rumus untuk mencari luas segitiga. Semua inti dari rumusnya adalah L= \frac{1}{2} \times a \times t.

Bagaimana mencari luas bangun datar tersebut?

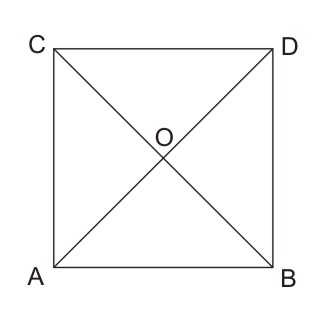
Bentuk bangun datar tersebut adalah bentuk persegi. Yang panjang setiap sisinya adalah sama. Perhatikan persegi tersebut. Kita bisa memandangnya sebagai 4 buah segitiga. Yaitu segitiga ABO, segitiga BOD, segitiga DOC dan segitiga COA.. Bentuk persegi tersebut adalah segi empat yang beraturan. Mempunyai panjang DO, CO, AO, BO sama.

 

Lalu bagaimana mencari luasnya dengan mencari luas segitiga yang membentuknya?

 

Luas masing-masing segitiga tersebut adalah sama. Karena bangun datar ini adalah segiempat beraturan (persegi). Luas AOB sama dengan

  

\frac{1}{2} \times AO \times BO.

  

Sehingga luas segi empat beraturan adalah L= 4 \times \frac{1}{2} \times AO \times BO.

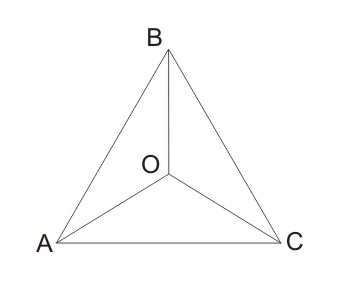
Bagaimana untuk segitiga beraturan?

Sama halnya dengan segiempat beraturan. Untuk mencari luas segitiga beraturan juga bias didapatkan dari mencari luas segitiga yang membentuknya. Luas AOB sama dengan

\frac{1}{2} \times AO \times BO \times sin(120).

Sehingga luas segi tiga beraturan adalah L= 3 \times \frac{1}{2} \times AO \times BO \times sin(120).

Perhatikan lagi untuk luas segiempat beraturan. L= 4 \times \frac{1}{2} \times AO \times BO. Bentuk tersebut juga bias dituliskan L= 4 \times \frac{1}{2} \times AO \times BO \times sin(90). Karena sin(90)=1.

Dari konsep tersebut, kita bisa menentukan rumus untuk segi lima beraturan, segi enam beraturan, segi tujuh beraturan, segi delapan beraturan, dan luas segi n beraturan. Yaitu sebagai berikut.

L= n \times \frac{1}{2} \times r^2 \times sin( \frac{360}{n}).

Itu adalah rumus untuk segi-n beraturan. Jadi, untuk segitiga, ganti n dengan 3. Untuk segi empat, ganti n dengan empat. Untuk segilima, ganti n dengan 5, untuk segi enam, ganti n dengan 6, dan seterusnya. Ingat! ini hanya berlaku untuk segi n yang beraturan. Artinya setiap sisinya mempunyai panjang yang sama. r di sini adalah jarak pusat segi n dengan titik pada perpotongan sisi-sisinya


You are here: Home / rumus matematika / Rumus Jari-jari Lingkaran Dalam dan Lingkaran Luar Segitiga

Rumus Jari-jari Lingkaran Dalam dan Lingkaran Luar Segitiga

Lingkaran Dalam Segitiga

Kasus pada lingkaran dalam segitiga untuk tingkat sekolah menengah pertama, biasanya diperkenalkan rumus untuk mencari jari-jari lingkaran. Materi lingkaran dalam segitiga melibatkan dua bangun yaitu lingkaran dan segitiga. Materi pertama mengenai bangun lingkaran yang berada dalam segitiga. Perhatikan gambar berikut!

Lingkaran dalam dan luar segitiga

Rumus mencari jari-jari lingkaran dalam segitiga.

Rumus Jari-Jari Lingkaran Dalam Segitiga

  \[ r = \frac{L_{\Delta ABC}}{s} \]

dengan s = \frac{1}{2} \left(a + b + c \right)

 

Selanjutnya adalah pembahasan lingkaran luar segitiga.

 

Lingkaran Luar Segitiga

Pembahasan di sini masih sama dengan pembahasan sebelumunya, yaitu melibatkan lingkaran dan segitiga. Hanya saja, lingkaran yang diberikan pada pembahasan ini berada di luar segitiga. Seperti judulnya “lingkaran luar segitiga” artinya ada lingkaran diluar segitiga. Ketiga titik sudut pada segitiga tersebut terletak pada lingkaran. Secara lebih jelasnya, perhatikan gambar di bawah!

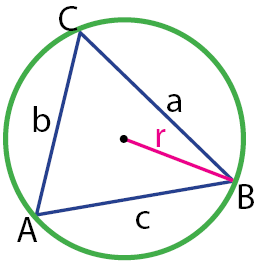
lingkaran dalam dan luar segitiga

Persamaan di bawah merupakan rumus mencari jari-jari lingkaran luar segitiga.

Rumus Jari-Jari Lingkaran Luar Segitiga

  \[ r = \frac{AB \times AC \times BC}{4 \times L_{\Delta ABC}}\]

atau

  \[ r = \frac{abc}{4 \times L_{\Delta ABC}}\]

 

Garis Singgung Lingkaran

Garis Singgung Persekutuan Dalam Dua Lingkaran

Seperti halnya garis singgung persekutuan luas dua lingkaran, garis singgung persekutuan dalam dua lingkaran juga melibatkan dua buah lingkaran dan sebuah garis singgung. Bedanya terletak pada posisi garis singgung lingkaran. Dua titik singgung lingkaran pada garis singgung persekutuan luar dua lingkaran terletak di sisi yang sama. Sedangkan dua titik singgung lingkaran pada garis singggung persekutuan dalam dua lingkaran terletak bersebrangan. Untuk lebih jelasnya, perhatikan gambar di bawah!
 
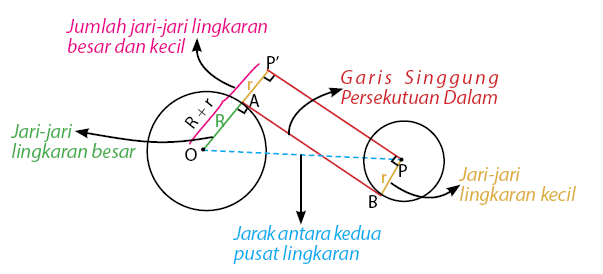
Garis singgung lingkaran
 

Sama halnya dengan garis singgung persekutuan dalam, garis singgung persekutuan luar juga didapat dengan menerapkan konsep teorema phytagoras.

Perhatikan bahwa segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Dengan teorema phytagoras dapat diperoleh panjang PP’ yaitu sebagai berikut.

  \[ PP' = \sqrt{OP^{2}-\left( OP'\right)^{2}} \]

Karena OP' = OA + BP = R + r maka,

  \[ PP' = \sqrt{OP^{2} - \left( R + r\right)^{2}} \]

 

Sehingga, rumus garis singgung persekutuan dalam dua llingkaran dapat dinyatakan dalam rumus di bawah.

Rumus mencari panjang garis singgung persekutuan dalam

  \[ AB = PP' = \sqrt{OP^{2} - (R + r)^{2}} \]

Keterangan:
        AB = PP’ = Garis singgung persekutuan luar lingkaran
        OP = Jarak antara kedua pusat lingkaran
        R = Jari-jari lingkaran besar
        r = jari-jari lingkaran kecil
 

Begitulah rumus mencari garis singgung lingkaran yang melibatkan dua lingkaran. Selanjutnya, sobat idschool dapat menyimak contoh soal garis singgung persekutuan luar lingkaran dan garis singgung persekutuan dalam lingkaran.

 

Komentar

Posting Komentar

Postingan populer dari blog ini

FUNGSI TRIGONOMETRI DAN BEBERAPA CONTOH SOALNYA

Gambar
 NAMA : CHAMELIA CHANSA  ABSEN : 08 KELAS : XIPS3 Pengertian Fungsi Trigonometri Jenis-jenis fungsi trigonometri Persamaan Trigonometri Berikut adalah rumus dari persamaan trigonometri: Sumber: Dokumentasi penulis Tabel Trigonometri Berikut adalah tabel trigonometri pada kuadran I Sumber: Dokumentasi penulis Berikut adalah tabel tabel trigonometri pada kuadran II Sumber: Dokumentasi penulis Berikut adalah tabel tabel trigonometri pada kuadran III Sumber: Dokumentasi penulis Berikut adalah tabel tabel trigonometri pada kuadran IV Sumber: Dokumentasi penulis Hal-hal yang perlu diperhatikan dalam fungsi trigonometri diantaranya: Sumber: Dokumentasi penulis Rumus dasar trigonometri sin 2  A + cos 2  A = 1 1 + cot 2  A = csc 2  A tan 2  A + 1 = sec 2  A Rumus trigonometri (jumlah dan selisih sudut) Sumber: Dokumentasi penulis Rumus trigonometri perkalian Sumber: Dokumentasi penulis Sifat-sifat trigonometri Sifat trigonometri fleksibel dia dapat diubah kebentuk persamaan kuadrat yang bisa di
Baca selengkapnya

PERSAMAAN LINEAR TIGA VARIABEL

Gambar
 NAMA : CHAMELIA CHANSA  KELAS : X IPS 3 ABSEN : 07 PERSAMAAN LINEAR TIGA VARIABLE { SPLTV} Sistem persamaan linear tiga variabel (SPLTV) adalah sebuah persamaan matematika yang meliputi 3 persamaan linear yang masing – masing dari persamaan yang bervariabel tiga (contoh x, y dan z). Dan SPLTV juga didefinisikan sebagai suatu bentuk konsep di dalam ilmu matematika yang bermanfaat untuk menyelesaikan sebuah kasus yang tidak bisa untuk diselesaikan dengan menggunakan bentuk persamaan linear satu variabel danjuga  persamaan linear dua variabel. Definisi Dan Bentuk Umum Sistem persamaan linear tiga variabel (SPLTV) adalah bentuk perluasan dari  persamaan linear dari dua variabel (SPLDV) Bentuk yang umum dari Sistem Persamaan Linear Tiga Variabel (SPLTV) di dalam x, y, dan juga z bisa ditulis seperti berikut ini : ax + by + cz = d                                  a 1 x + b 1 y + c 1 z = d 1 ex + fy + gz = h             atau              a 2 x + b 2 y + c 2 z = d  2 ix + jy + kz = l         
Baca selengkapnya