SOAL PERSAMAAN DAN PERTIDAKSAMAAN RASIONAL DAN IRASIONAL

 Soal persamaan dan pertidaksamaan rasional dan irasional

1. Penyelesaian √2x+6>0 adalah ⋯⋅

A. x<3                              D. x>−3
B. x≤−3                           E. x>6
C. x≥−3 

Diketahui √2x+6>0.
Kuadratkan kedua ruas, lalu selesaikan.
(√2x+6)2>(0)22x+6>02x>−6x>−3

Syarat akar:

2x+6≥0⇔x≥−3
Karena semua x yang memenuhi x>−3 juga memenuhi syarat akar x≥−3, maka penyelesaian pertidaksamaan tersebut adalah x>−3
(Jawaban D)

2. Jika pertidaksama √3−ax≤2 dipenuhi oleh interval a−2≤x≤3, maka nilai a2−a=⋯⋅

A. 4                      C. 2                  E. 0
B. 3                      D. 1          

Pembahasan:

Diketahui √3−ax≤2.
Kuadratkan kedua ruas untuk memperoleh 3−ax≤4.
Syarat akar: 3−ax≥0.
Dari sini, kita peroleh
0≤3−ax≤4−3≤−ax≤1−1a≤x≤3a
Karena diketahui bahwa pertidaksamaan √3−ax≤2 terpenuhi oleh interval a−2≤x≤3, maka jelas bahwa a=1.
Dengan demikian, nilai dari a2−a=(1)2−1=0
(Jawaban E)

3.Jika √3x−1<2, maka nilai x yang memenuhi pertidaksamaan tersebut adalah ⋯⋅

A. x<53                          D. 13<x<53
B. x>13                          E. 13<x≤53
C. 13≤x<53

Pembahasan:

Diketahui $\sqrt{3x-1}<2$.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cccc}(\sqrt{3x-1}{)}^2& <(2{)}^2& & \\ 3x-1& <4& & \\ 3x& <5& & \\ x& <\frac{5}{3}& & \left(★\right)\end{array}$
Syarat akar:
$3x-1\ge 0\iff x\ge \frac{1}{3}$
Gunakan garis bilangan.

Irisan dari $★$ dan syarat akar di atas merupakan penyelesaian pertidaksamaan.
Tampak bahwa irisan dari $\left(1\right)$ dan $\left(2\right)$ adalah $\frac{1}{3}\le x<\frac{5}{3}$
(Jawaban C)

4. Nilai x yang memenuhi pertidaksamaan √2x2+6x−8<√x2+6x adalah ⋯⋅
A. {x | 0≤x<2√2}
B. {x | 1≤x<2√2}
C. {x | x>2√2}
D. {x | x≥1}
E. {x | x≥0}

Pembahasan:

Diketahui √2x2+6x−8<√x2+6x.
Kuadratkan kedua ruas, lalu selesaikan.
(√2x2+6x−8)2<(√x2+6x)22x2+\cancel6x−8<x2+\cancel6xx2−8<0(x−2√2)(x+2√2)<0
Pembuat nol: x=−2√2 atau x=2√2.
Penyelesaiannya adalah −2√2<x<2√2    (★)
Syarat akar (1):
2x2+6x−8≥0⇔2(x+4)(x−1)≥0
Pembuat nol: x=−4 atau x=1.
Penyelesaiannya adalah x≤−4 atau x≥1.
Syarat akar (2):
x2+6x≥0⇔x(x+6)≥0
Pembuat nol: x=0 atau x=−6.
Penyelesaiannya adalah x≤−6 atau x≥0.
Gunakan garis bilangan.

Irisan dari ★ dan kedua syarat akar di atas merupakan himpunan penyelesaian pertidaksamaan.
Tampak bahwa irisannya adalah {x | 1≤x<2√2}

(Jawaban B)

5. Himpunan penyelesaian √x2−3x+2≤√x+7 adalah ⋯⋅

Pembahasan: 

Diketahui √x2−3x+2≤√x+7.
Kuadratkan kedua ruas, lalu selesaikan.
(√x2−3x+2)2≤(√x+7)2x2−3x+2≤x+7x2−4x−5≤0(x+1)(x−5)≤0
Pembuat nol: x=−1 atau x=5.
Penyelesaiannya adalah −1≤x≤5    (★)
Syarat akar (1):
x2−3x+2≥0⇔(x−1)(x−2)≥0
Pembuat nol: x=1 atau x=2.
Penyelesaiannya adalah x≤1 atau x≥2.
Syarat akar (2):
x+7≥0⇔x≥−7
Gunakan garis bilangan.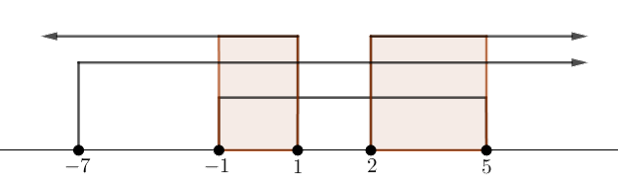

Irisan dari ★ dan kedua syarat akar di atas merupakan himpunan penyelesaian pertidaksamaan.
Tampak bahwa irisannya adalah {x |−1≤x≤1 atau 2≤x≤5,x∈R}
(Jawaban D)

$x>\sqrt{x+12}$, nilai $x$ yang memenuhi adalah $\cdots \cdot$
A. $-12<x<-3$ atau $x>4$                  
B. $x<-3$ atau $x>4$                         
C. $x<-12$
D. $x>0$
E. $x>4$

pembahasan

Diketahui $x>\sqrt{x+12}$.
Ruas kiri pada pertidaksamaan di atas belum tentu bernilai non-negatif. Oleh karena itu, perlu diuraikan menjadi dua kemungkinan, yaitu $x<0$ dan $x\ge 0$.
Kasus 1: $x<0$
Oleh karena $\sqrt{x+12}\ge 0$ dan $x<0$, maka $x>\sqrt{x+12}$ tidak akan memiliki penyelesaian untuk setiap $x$.
Kasus 2: $x\ge 0$
Oleh karena $x\ge 0$, maka kedua ruas pada pertidaksamaan tersebut tidak bernilai negatif sehingga boleh dikuadratkan.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cc}(x{)}^2& >(\sqrt{x+12}{)}^2\\ x^2& >x+12\\ x^2-x-12& >0\\ (x+3)(x-4)& >0\end{array}$
Pembuat nol: $x=-3$ atau $x=4$.
Penyelesaiannya adalah $x<-3\text{atau}x>4\left(★\right)$
Syarat akar $\left(1\right)$: $x\ge 0$
Syarat akar $\left(2\right)$:
$x+12\ge 0\iff x\ge -12$

Irisan dari $★$ dan kedua syarat akar di atas merupakan himpunan penyelesaian pertidaksamaan.
Tampak bahwa irisannya adalah $x>4$
(Jawaban E)

7.

pembahasan : 

8.

 

pembahasan :

9.

pembahasan:

10.

pembahasan :

11. tentukan himpunan penyelesaian dari setiap pertidaksamaan berikut ini: 

Jawab: 

12.Tentukan himpunan penyelesaian dari  :

Jawab:

Pembuat nol adalah
x − 3 = 0  ⇒ x = 3
x + 1 = 0  ⇒ x = −1

Syarat :
x + 1 ≠ 0  ⇒ x ≠ −1

Untuk interval x < −1, ambil x = −2 : 

Untuk interval −1 < x ≤ 3, ambil x = 0 : 

Untuk interval x > 3, ambil x = 4 : 

Sebab pertidaksamaan bertanda “≥”, maka daerah penyelesaiannya berada pada interval yang bertanda positif (+).
Yaitu: HP = {x < −1 atau x ≥ 3}

13.  Tentukan himpunan penyelesaian dari  :

Jawab :

Pembuat nol adalah
(x − 1)(x − 1) = 0  ⇒ x = 1
x + 2 = 0  ⇒ x = −2

Syarat :
x + 2 ≠ 0  ⇒ x ≠ −2

Sebab pertidaksamaan bertanda “<“, maka daerah penyelesaian berada pada interval yang bertanda negatif (−).
Yaitu Himpunan Penyelesaian = {x < −2}

14.  Tentukan HP dari 

$\frac{x-3}{x+1}$ ≥ 0

Jawab :
Pembuat nol :
x − 3 = 0  ⇒ x = 3
x + 1 = 0  ⇒ x = −1

Syarat :
x + 1 ≠ 0  ⇒ x ≠ −1

Untuk interval x < −1, ambil x = −2 :
$\frac{-2-3}{-2+1}$ = 5 (+)

Untuk interval −1 < x ≤ 3, ambil x = 0 :
$\frac{0-3}{0+1}$ = −3 (−)

Untuk interval x > 3, ambil x = 4 :
$\frac{4-3}{4+1}$ = $\frac{1}{5}$ (+)

Karena pertidaksamaan bertanda "≥", maka daerah penyelesaian berada pada interval yang bertanda (+).

∴ HP = {x < −1 atau x ≥ 3}

15. Tentukan HP dari 

$\frac{2x-1}{4-x}$ > 0

Jawab :
Pembuat nol :
2x − 1 = 0  ⇒ x = $\frac{1}{2}$
4 − x = 0  ⇒ x = 4

Syarat :
4 − x ≠ 0  ⇒ x ≠ 4

Karena pertidaksamaan bertanda ">", maka daerah penyelesaian berada pada interval yang bertanda (+).

∴ HP = {$\frac{1}{2}$ < x < 4}

16.  Tentukan HP dari 

$\frac{x^2-2x+1}{x+2}<0$

Jawab :
$\frac{(x-1)(x-1)}{x+2}<0$

Pembuat nol :
(x − 1)(x − 1) = 0  ⇒ x = 1
x + 2 = 0  ⇒ x = −2

Syarat :
x + 2 ≠ 0  ⇒ x ≠ −2

Karena pertidaksamaan bertanda "<", maka daerah penyelesaian berada pada interval yang bertanda (−).

∴ HP = {x < −2}

17.Tentukan HP dari $\frac{x-5}{x^2+6x+9}\le 0$

Jawab :

$\frac{x-5}{(x+3)(x+3)}\le 0$

Pembuat nol :
x − 5 = 0  ⇒ x = 5
(x + 3)(x + 3) = 0  ⇒ x = −3

Syarat :
(x + 3)(x + 3) ≠ 0  ⇒ x ≠ −3

Karena pertidaksamaan bertanda "≤", maka daerah penyelesaian berada pada interval yang bertanda (−).

∴ HP = {x < −3 atau −3 < x ≤ 5} atau
   HP = {x ≤ 5 dan x ≠ −3}

18. Tentukan HP dari 

$\frac{x+1}{x-2}\ge \frac{1}{x-1}$

Jawab :
⇔ $\frac{x+1}{x-2}-\frac{1}{x-1}$ ≥ 0
⇔ $\frac{(x+1)(x-1)-(x-2)}{(x-2)(x-1)}$ ≥ 0
⇔ $\frac{x^2-1-x+2}{(x-2)(x-1)}$ ≥ 0
⇔ $\frac{x^2-x+1}{(x-2)(x-1)}$ ≥ 0

x² − x + 1 merupakan fungsi definit positif, sehingga dapat diabaikan tanpa harus mengubah atau membalik tanda pertidaksamaan.

Jadi pertidaksamaan diatas setara dengan
$\frac{1}{(x-2)(x-1)}$ ≥ 0

Pembuat nol :
(x − 2)(x − 1) = 0  ⇒ x = 2 atau x = 1

Syarat :
(x − 2)(x − 1) ≠ 0  ⇒ x ≠ 2 atau x ≠ 1

Karena pertidaksamaan bertanda "≥", maka daerah penyelesaian berada pada interval yang bertanda (+).
∴ HP = {x < 1 atau x > 2}

19. Tentukan HP dari 

$\frac{2x-1}{x+2}\ge 1$

Jawab :
⇔ $\frac{2x-1}{x+2}$ − 1 ≥ 0
⇔ $\frac{2x-1}{x+2}-\frac{x+2}{x+2}$ ≥ 0
⇔ $\frac{2x-1-x-2}{x+2}$ ≥ 0
⇔ $\frac{x-3}{x+2}$ ≥ 0

Pembuat nol :
x − 3 = 0  ⇒ x = 3
x + 2 = 0  ⇒ x = −2

Syarat :
x + 2 ≠ 0  ⇒ x ≠ −2

Karena pertidaksamaan bertanda "≥", maka daerah penyelesaian berada pada interval yang bertanda (+).
∴ HP = {x < −2 atau x ≥ 3}

20. Tentukan HP dari 

$\frac{4}{-x^2-4}\ge \frac{1}{x-1}$

Jawab :
⇔ $\frac{4}{-x^2-4}-\frac{1}{x-1}$ ≥ 0
⇔ $\frac{4(x-1)-(-x^2-4)}{(-x^2-4)(x-1)}$ ≥ 0
⇔ $\frac{4x-4+x^2+4}{(-x^2-4)(x-1)}$ ≥ 0
⇔ $\frac{x^2+4x}{(-x^2-4)(x-1)}$ ≥ 0
⇔ $\frac{x(x+4)}{(-x^2-4)(x-1)}$ ≥ 0

−x² − 4 merupakan fungsi definit negatif sehingga dapat diabaikan dengan syarat tanda pertidaksamaan diubah atau dibalik.

Jadi pertidaksamaan diatas setara dengan
$\frac{x(x+4)}{x-1}$ ≤ 0

Pembuat nol :
x(x + 4) = 0  ⇒ x = 0 atau x = −4
x − 1 = 0  ⇒ x = 1

Syarat :
x − 1 ≠ 0  ⇒ x ≠ 1

Karena pertidaksamaan bertanda "≤" maka daerah penyelesaian berada pada interval yang bertanda (−).
∴ HP = {x ≤ −4 atau 0 ≤ x < 1}