NAMA  : CHAMELIA CHANSA 

KELAS : X IPS 3

ABSEN : 08

SUDUT-SUDUT BERELASI

Sudut-sudut yang berelasi atau berhubungan ditunjukkan dengan adanya hubungan antara sudut α dengan sudut (90° ± α), (180° ± α), (270° ± α), (360° ± α), atau -α.

Jika sudut α berelasi dengan sudut (90° - α) atau (π2 - α), maka kedua sudut dinamakan saling berpenyiku. Selanjutnya, jika sudut α berelasi dengan sudut (180° - α) atau (π - α), maka kedua sudut tersebut dinamakan saling berpelurus.

Perbandingan Trigonometri di Kuadran I

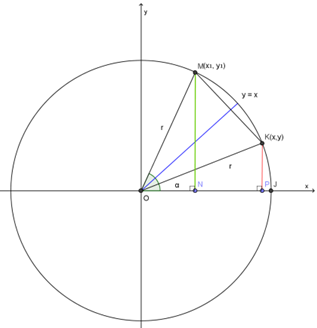
Oleh karena pada gambar di atas, titik M(x1, y1) adalah bayangan dari titik K(x, y) oleh pencerminkan terhadap garis y = x, maka

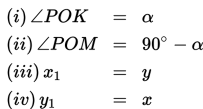
Dengan demikian, relasi antara sudut α dengan sudut (90° - α) atau (π2−α) adalah sebagai berikut:

Contoh:

• sin75°=sin(90°−15°)=cos15°
• cosπ6=cos(π2−π3)=sinπ3
• tan25°=tan(90°−65°)=cot65°

Perbandingan Trigonometri di Kuadran II

A. Sudut α berelasi dengan sudut (180° - α) atau (π - α)

Relasi antara sudut α dengan sudut (180° - α) adalah sebagai berikut:

Contoh:

• sin120°=sin(180°−60°)=sin60°=123√
• cos56π=cos(π−π6)=−cosπ6=−123√
• tan135°=tan(180°−45°)=−tan45°=−1

B. Sudut α berelasi dengan (90° + α) atau (π2 + α)

Misalkan A(x , y), OA = r, dan ∠AOC = α.

Jika α diputar dengan pusat perputaran adalah O(0,0) sejauh 90° dengan arah berlawanan arah putar jarum jam, maka bayangan titik A oleh perputaran tersebut adalah A'(-y , x).

Dengan demikian, ∠AOA' = (90° + α) dan OA = OA' = r.

Berdasarkan gambar di atas, relasi antara sudut α dengan (90° + α) adalah sebagai berikut:

Contoh:

• sin 120° = sin(90° + 30°) = cos 30° = 123√
• tan 135° = tan(90° + 45°) = - cot 45° = -1

Perbandingan Trigonometri di Kuadran III

A. Sudut α berelasi dengan (180° + α) atau (π + α)

Mari kita perhatikan gambar berikut.

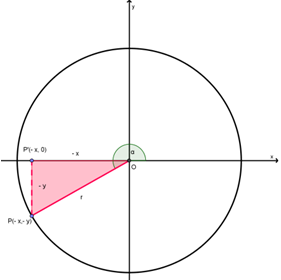
Relasi antara sudut α dengan sudut (180° + α) adalah sebagai berikut:

B. Sudut α berelasi dengan sudut (270° - α) atau (32π - α)

Misalkan A(x , y), OA = r, dan ∠AOC = α.

Jika titik A dicerminkan terhadap garis y = x, kemudian diputar dengan pusat perputaran adalah O sejauh 180° dengan arah berlawanan arah putar jarum jam, maka bayangan dari titik A adalah A"(-y, -x), dimana ∠AOA' = (270° - α) dan OA = OA" = r.

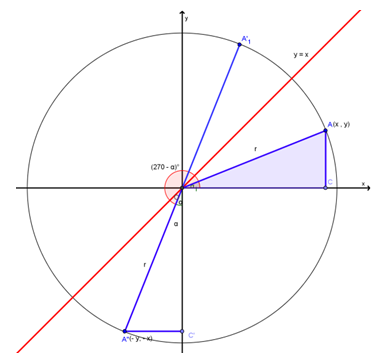
Berdasarkan gambar di atas, relasi antara sudut α dengan (270° - α) adalah sebagai berikut:

Contoh:

Tentukan nilai dari cos 210° dengan menggunakan relasi (180° + α) dan (270° - α).

Penyelesaian:

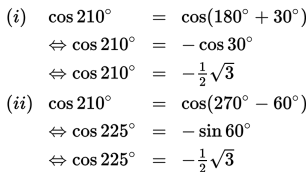
Berdasarkan uraian di atas, tampak bahwa kedua relasi memberikan hasil yang sama.

Perbandingan Trigonometri di Kuadran IV

A. Sudut α berelasi dengan (360° - α) atau (2π - α)

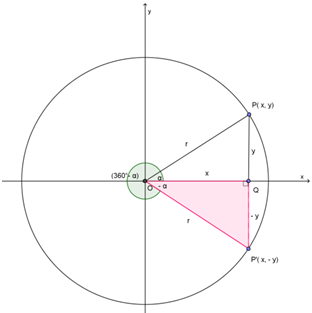
Berdasarkan gambar di atas,

• ∠QOP = α
• ∠QOP' = (360° - α)

Dengan demikian, relasi antara sudut α dengan sudut (360° - α) atau (2π - α) adalah sebagai berikut:

Contoh:

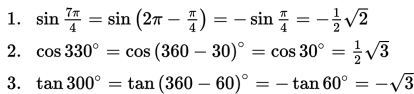
B. Sudut α berelasi dengan sudut (270° + α) atau (32π + α)

Jika titik A(x , y) dengan OA = r dan ∠AOB = α diputar dengan pusat O(0,0) sejauh 270° dengan arah berlawanan arah putar jarum jam, maka bayangan dari titik A adalah A'(y , x), dimana∠AOA' = (270° + α) dan OA = OA' = r.

Berdasarkan gambar di atas, relasi antara sudut α dan sudut (270° + α) adalah sebagai berikut:

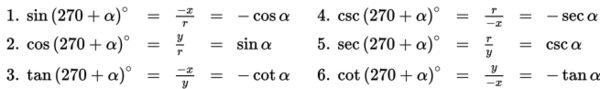
C. Sudut α berelasi dengan sudut (-α)

Mari kita perhatikan gambar berikut.

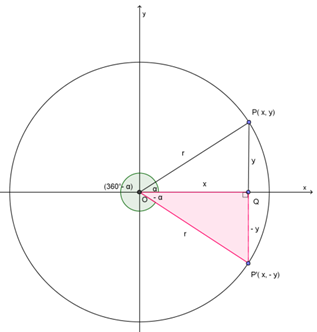
Pada gambar di atas,

• ∠QOP = α → berlawanan arah dengan arah putar jarum jam
• ∠QOP' = -α → searah dengan arah putar jarum jam

Dengan demikian,

Contoh:

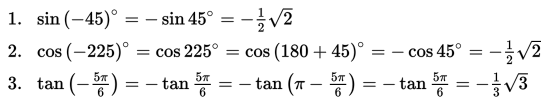
Bagaimana dengan nilai perbandingan trigonometri pada batas kuadran?
Nilai perbandingan trigonometri pada batas kuadran dapat kita tentukan dengan menggunakan lingkaran satuan.

Lantas, bagaimana dengan sudut A yang lebih besar dari 360°?

Jika sudut A lebih besar dari 360°, maka sudut A harus diubah terlebih dahulu sehingga berbentuk (θ + k.360°) dengan k = 1, 2, 3, 4, ....

Dengan demikian,