SOAL DAN PEMBAHASAN FUNGSI TRIGONOMETRI

 NAMA : CHAMELIA CHANSA 

ABSEN : 08

KELAS : X IPS 3

Contoh Soal Fungsi Trigonometri

1 . Diketahui grafik fungsi $y_1=5\sin x$ dan $y_2=\sin 5x$. Pernyataan berikut yang benar adalah $\cdots \cdot$
A. periode $y_1$ = periode $y_2$
B. amplitudo $y_1$ = amplitudo $y_2$
C. periode $y_1=\frac{1}{5}$ kali periode $y_2$
D. amplitudo $y_1=\frac{1}{5}$ kali amplitudo $y_2$
E. amplitudo $y_1=5$ kali amplitudo $y_2$

Pembahasan

Bentuk umum fungsi sinus tersebut adalah $y=a\sin kx$.
Periode:
Periode $y_1=5\sin x$ dengan $k=1$ adalah $P_1=\frac{{360}^{\circ }}{1}={360}^{\circ }$, sedangkan periode $y_2=\sin 5x$ dengan $k=5$ adalah $P_2=\frac{{360}^{\circ }}{5}={72}^{\circ }$.
Dapat disimpulkan bahwa periode $y_1$ sama dengan 5 kali periode $y_2$.
Amplitudo:
Amplitudo $y_1=5\sin x$ dengan $a=5$ adalah $A_1=|a|=|5|=5$, sedangkan amplitudo $y_2=\sin 5x$ dengan $a=1$ adalah $A_2=|a|=|1|=1$. Dapat disimpulkan bahwa amplitudo $y_1$ 5 kali amplitudo $y_2$.
Pernyataan yang benar ada pada pilihan E.

2. Perhatikan grafik berikut.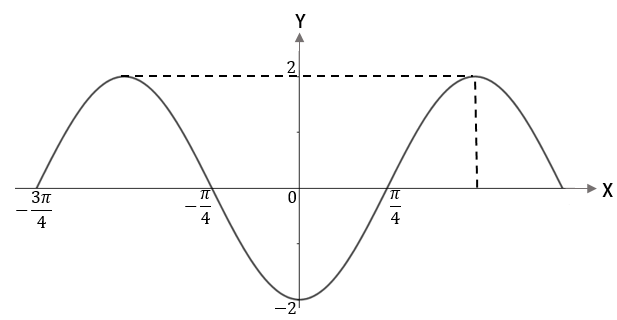

Fungsi yang memenuhi grafik di atas adalah $\cdots \cdot$
A. $f\left(x\right)=-2\sin (x-\frac{\pi }{4})$
B. $f\left(x\right)=-2\sin (x+\frac{\pi }{4})$
C. $f\left(x\right)=-2\sin (2x-\frac{\pi }{2})$
D. $f\left(x\right)=-2\sin (2x+\frac{\pi }{2})$
E. $f\left(x\right)=-2\sin (2x-\frac{\pi }{4})$

Pembahasan

Beranjak dari grafik sinus: karena kurva bergeser (ke kiri) sejauh $\frac{\pi }{4}$, maka bentuk umum grafik fungsinya adalah $f\left(x\right)=y=a\sin k(x-c)$.
Untuk grafik ini, nilai $c$ yang menentukan pergeseran kurva adalah $-\frac{\pi }{4}$.
Dimulai dari titik $x=-\frac{3\pi }{4}$ yang nilai fungsinya 0, grafik fungsi kembali bernilai $0$ dan berulang kembali di titik $x=\frac{\pi }{4}$, sehingga periode grafik fungsinya adalah $\frac{\pi }{4}–(-\frac{3\pi }{4})=\pi$.
Dengan demikian,
$k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{\pi }=2$
Nilai $a$ ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{2-(-2)}{2}=2\end{array}$
Catatan: Pilihan ganda pada soal menunjukkan bahwa $a=-2$, artinya kurva sinus menurun, lalu menanjak. Ini menjadi alasan mengapa kita anggap kurva bergeser ke kiri.
Jadi, rumus grafik fungsinya adalah$$f\left(x\right)=-2\sin 2(x+\frac{\pi }{4})=-2\sin (2x+\frac{\pi }{2})$$(Jawaban D)

4. Grafik $f\left(x\right)=2\cos x$ memotong sumbu-$X$ di titik berkoordinat $\cdots \cdot$
A. $({30}^{\circ },0)$              D. $({90}^{\circ },0)$
B. $({45}^{\circ },0)$              E. $({180}^{\circ },0)$
C. $({60}^{\circ },0)$

Pembahasan

Apabila grafik memotong sumbu-$X$, maka nilai $f\left(x\right)=y=0$. Dengan demikian,
$f\left(x\right)=2\cos x\Rightarrow 0=2\cos x\iff \cos x=0$
Nilai $x$ yang membuat $\cos x$ bernilai 0 adalah ${90}^{\circ }$.
Jadi, titik potong grafiknya berkoordinat $({90}^{\circ },0)$
(Jawaban D)

5. diketahui persamaan trigonometri sin 2x = cos 3x,  maka himpunan penyelesaiannya adalah….

Pembahasan:

sin 2x = cos 3x

sin 2x = sin (90° – 3x)

2x = 90° – 3x + k 360°

5x = 90° + k 360°

5x = 90° x = 18

Atau 5x = 90° + 360° x = 90

atau 5x = 90° + 720° x = 162

atau 5x = 90° + 1080° x = 234

Atau 5x = 90° + 1440° x = 306

Himpunan penyelesaian dari sin 2x = cos 3x adalah (18°, 90°, 162°, 234°, 306°).

 

5. Tentukan himpunan penyelesaian dari persamaan 2 sin² 3x + 2 sin 3x = -4 !

Pembahasan:

2 sin² 3x + 2 sin 3x = -4

2 sin² 3x + 2 sin 3x + 4 = 0

sin² 3x + sin 3x + 2 = 0

(sin 3x + 2)(sin 3x – 1) = 0

sin 3x + 2 sin 3x = -2 (tidak bisa)

Atau sin 3x – 1 sin 3x = 1 = sin 90 3x = 90 x  = 30

Himpunan penyelesaian dari 2 sin² 3x + 2 sin 3x = -4 adalah (30°).

 

6 . Tentukan himpunan penyelesaian dari persamaan 3 cos x + 4 sin x = 5.

Pembahasan:

Rumus trigonometri

7.  Diketahui 

$f\left(x\right)=\sqrt{2}\cos 3x+1$. Jika nilai maksimum dan minimum $f\left(x\right)$ berturut-turut adalah $p$ dan $q$, maka nilai $p^2+q^2$ adalah $\cdots \cdot$
A. $1$                     C. $3$                     E. $6$
B. $2$                     D. $4$           

Pembahasan

Nilai maksimum $f\left(x\right)=\sqrt{2}\cos 3x+1$ tercapai ketika $\cos 3x$ bernilai sebesar-besarnya, yaitu $\cos 3x=1$. Untuk itu,
$f_{\text{maks}}\left(x\right)=p=\sqrt{2}\left(1\right)+1=\sqrt{2}+1$
Nilai minimum $f\left(x\right)=\sqrt{2}\cos 3x+1$ tercapai ketika $\cos 3x$ bernilai sekecil-kecilnya, yaitu $\cos 3x=-1$. Untuk itu,
$f_{\text{min}}(x{)}_{=}q=\sqrt{2}(-1)+1=-\sqrt{2}+1$
Dengan demikian,
$\begin{array}{cc}{p}^2+q^2& =(\sqrt{2}+1{)}^2+(-\sqrt{2}+1{)}^2\\ & =(2+2\sqrt{2}+1)+(2–2\sqrt{2}+1)\\ & =6\end{array}$
Jadi, nilai dari $p^2+q^2=6$
(Jawaban E)